您好,您的问题似乎是关于某个数值的计算。根据您提供的信息“6.02n1.76”,我推测您可能是在询问一个数值的表示方法或者计算方式。然而,这个表达式本身并不完整,因为它缺少一些关键的信息,比如“n”的具体含义以及“6.02”和“1.76”之间的关系。
如果您是在询问某个物理常数或者科学概念,比如阿伏伽德罗常数(大约为6.02×10^23),那么您可能需要提供更多的上下文来解释“1.76”是如何与“6.02n”相关的。
如果您是在进行数学计算,那么您可能需要提供更多的信息,比如“n”的值,或者“6.02n1.76”代表的具体数学表达式。
请您提供更多的信息,以便我能够更准确地回答您的问题。
在电子工程领域,信噪比(SNR)是一个至关重要的性能指标,它直接关系到信号处理的准确性和可靠性。SNR的计算公式SNR=6.02N 1.76dB,经常出现在数据手册和学术论文中。本文将从多个维度深入解析这个公式,帮助读者更好地理解其背后的原理和应用。
公式的起源与意义
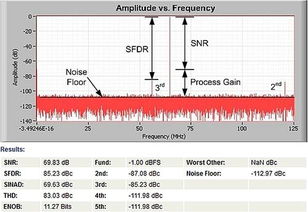
首先,让我们回顾一下SNR的定义。信噪比是指信号功率与噪声功率的比值,通常用分贝(dB)作为单位。在数字信号处理中,SNR的数值越高,表示信号质量越好,噪声干扰越小。
公式SNR=6.02N 1.76dB中的N代表ADC(模数转换器)的位数。这个公式源自于ADC的理论性能,即完美N位ADC的理论信噪比。它告诉我们,随着ADC位数的增加,理论信噪比也会相应提高。
公式的推导过程
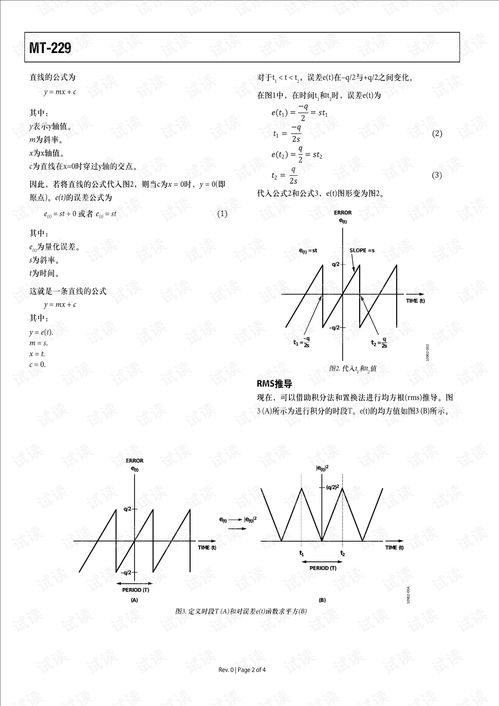
要理解这个公式,我们需要从量化噪声的角度入手。量化噪声是ADC在将模拟信号转换为数字信号时产生的误差。以下是一个简化的推导过程:
量化噪声电压的均方根值ΔV可以表示为ΔV=q/√12。将ΔV代入信噪比的定义公式SNR=20log10(Psignal/Pnoise),其中Psignal为信号功率,Pnoise为噪声功率,可以得到SNR的表达式。
经过一系列推导,最终得到SNR=6.02N 1.76dB。这个公式揭示了ADC位数与信噪比之间的关系,为工程师们提供了理论依据。
公式的应用与扩展

在实际应用中,SNR=6.02N 1.76dB公式可以帮助工程师们评估ADC的性能。例如,当需要选择一个ADC时,可以根据所需的信噪比和公式计算出所需的位数。
此外,该公式还可以扩展到其他领域。例如,在通信系统中,SNR也是衡量系统性能的重要指标。通过将SNR=6.02N 1.76dB公式应用于通信系统,可以评估系统的传输质量。
公式的局限性
尽管SNR=6.02N 1.76dB公式在理论上是成立的,但在实际应用中,它存在一定的局限性。首先,该公式只适用于完美N位ADC,而实际ADC存在量化误差、非线性失真等问题。其次,该公式未考虑过采样对SNR的影响。
因此,在实际应用中,工程师们需要根据具体情况对公式进行调整和修正,以获得更准确的SNR值。
SNR=6.02N 1.76dB公式是电子工程领域的一个重要公式,它揭示了ADC位数与信噪比之间的关系。通过深入理解该公式,工程师们可以更好地评估ADC的性能,为系统设计提供理论依据。然而,在实际应用中,工程师们需要根据具体情况对公式进行调整和修正,以获得更准确的SNR值。
